1003번: 피보나치 함수
Baekjoon Online Judge스타트링크 (Startlink)

이 문제는 간단한 다이나믹 문제라고 할 수 있습니다.

문제를 간단히 보게되면 문제에서 요구한 것 그 자체를 구현하기 쉽습니다.
하지만 문제를 그대로 구현하게되면 매번 달라지는 N에 대하여 재귀함수를 구성하는 것이 되고 그럴경우에는 시간복잡도가 터지게 됩니다.

그래서 이를 해소하기 위해서 다이나믹으로 미리 두개의 피보나치 수열을 만들어 놓는다면 수시로 다시 피보나치 수열을 반복해서 만들 필요가 없게 됩니다.

물론 일반적인 피보나치 수열을 전개하듯이 하게 되면 fibonacci(n)의 값이 N=2 까지는 일정하지 않게 됩니다.
그래서 이 경우를 위해 각 피보나치 수열의 값과 0,1의 출력되는 횟수를 고려하고 그에 대한 상관관계를 파악해야할 필요성이 있습니다.

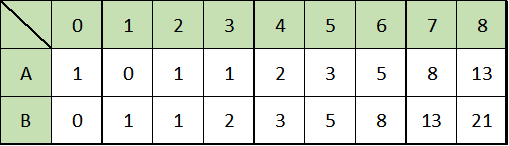
위를 보면 A라는 피보나치 수열과 B라는 피보나치 수열이 있습니다.
N에 따른 A 와 B의 출력횟수는 위와 같다고 할 수 있고 이를 이용한다면 두개의 배열을 활용해서 코드를 구성하는 법과 하나의 배열을 활용하는 법이 있을것이고 하나를 사용한다면 g[n-1], g[n] 를 사용해서 각각 A와 B를 출력할 수 있습니다.

#include<stdio.h>
int as[44][2]={0,};
int main()
{
    int i,n,t,j;
    as[0][0]=1,as[1][1]=1;
    scanf(“%d”,&t);
    for(j=0;j<t;j++)
    {
        scanf(“%d”,&n);
        for(i=2;i<=n;i++)
        {
            as[i][0]=as[i-1][0]+as[i-2][0];
            as[i][1]=as[i-1][1]+as[i-2][1];
        }
        printf(“%d %d\n”,as[n][0],as[n][1]);
    }
    return 0;
}